Линейные уравнения, содержащие параметр
![]() - таков общий вид названного уравнения.
- таков общий вид названного уравнения.
Его решение состоит из следующих частей:
1. Если ![]() , то
, то ![]() - единственный корень уравнения.
- единственный корень уравнения.
2. Если ![]() , то могут быть случаи:
, то могут быть случаи:
а) ![]() , уравнение решений не имеет;
, уравнение решений не имеет;
б) ![]() , любое число является корнем уравнения.
, любое число является корнем уравнения.
Результатом решения служит ответ:
1) ![]() ,
, ![]() - любое,
- любое, ![]() ;
;
2) ![]() ,
, ![]() ,
, ![]() - любое число.
- любое число.
3.1.1. Примеры линейных уравнений с параметрами
Пример 1. Решить уравнение ax = 1.
Решение. На первый взгляд представляется возможным сразу дать ответ:
х = ![]() . Однако при а = 0 данное уравнение решений не имеет, и верный ответ выглядит так:
. Однако при а = 0 данное уравнение решений не имеет, и верный ответ выглядит так:
Ответ: Если а = 0, то решений нет; если а ≠ 0, то х = ![]() .
.
Пример 2. Решить уравнение (а2 – 1)х = а + 1.
Решение. Рассмотрим случаи:
1) а = 1, тогда уравнение принимает вид 0х = 2 и не имеет решений;
2) а = -1,получаем 0х = 0, очевидно х – любое;
3) а ≠ ± 1; имеем х = ![]() .
.
Ответ: Если а = - 1, то х – любое; если а = 1, то нет решений; если а ≠ ± 1, то х = ![]() .
.
Пример 3: ![]()
После преобразования получаем равносильное данному уравнение
![]() .
.
-
Если
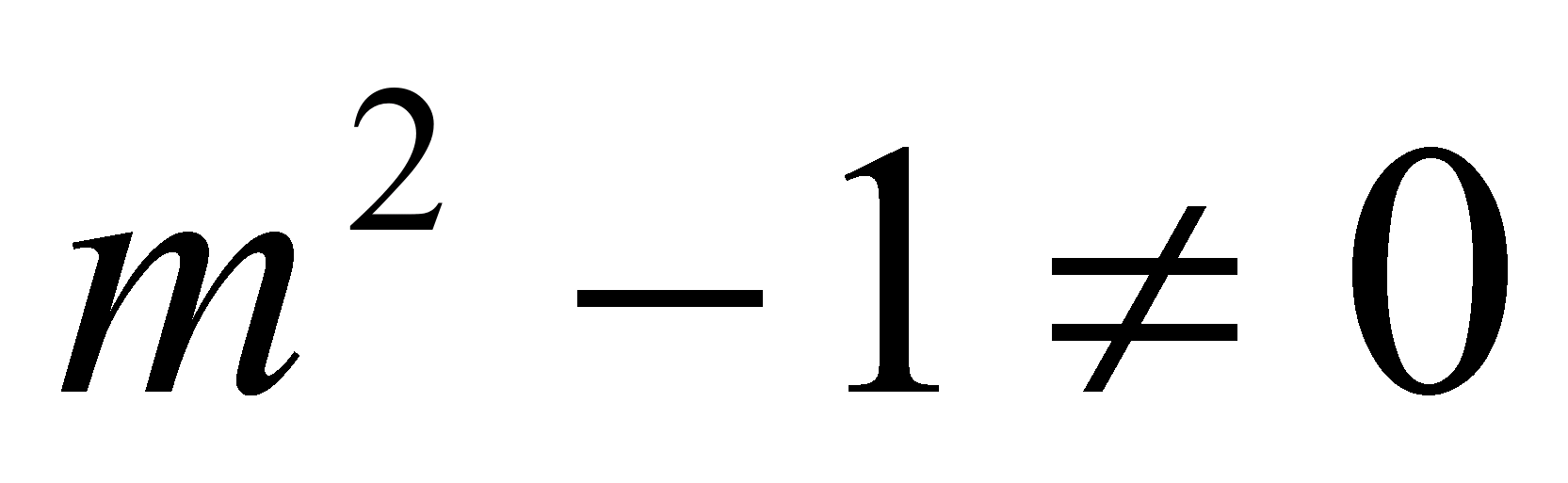 , т.е
, т.е 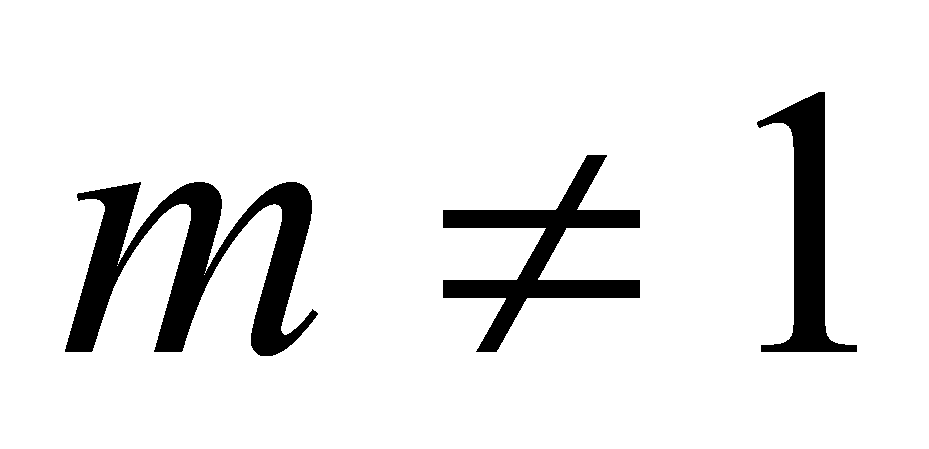 и
и 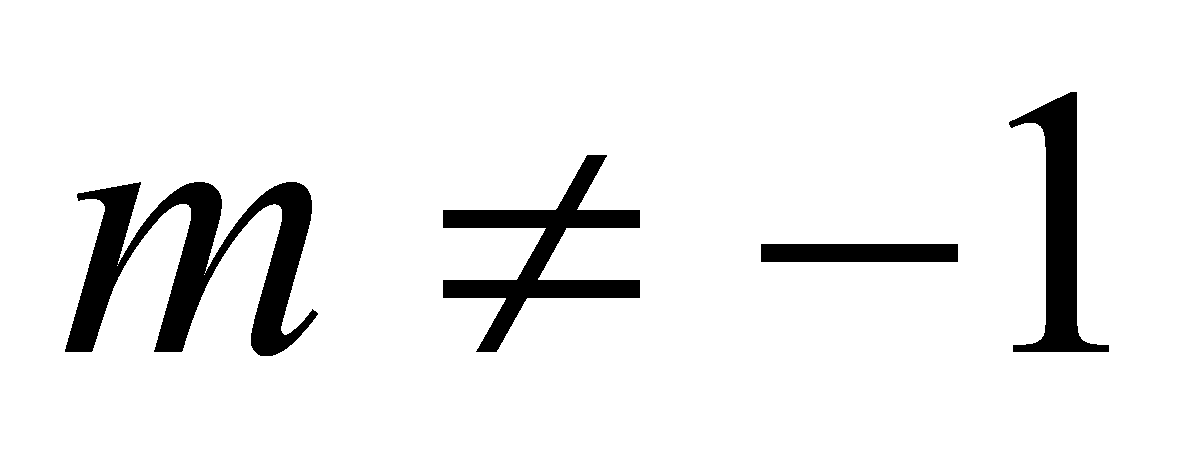 , то
, то
![]()
-
Если
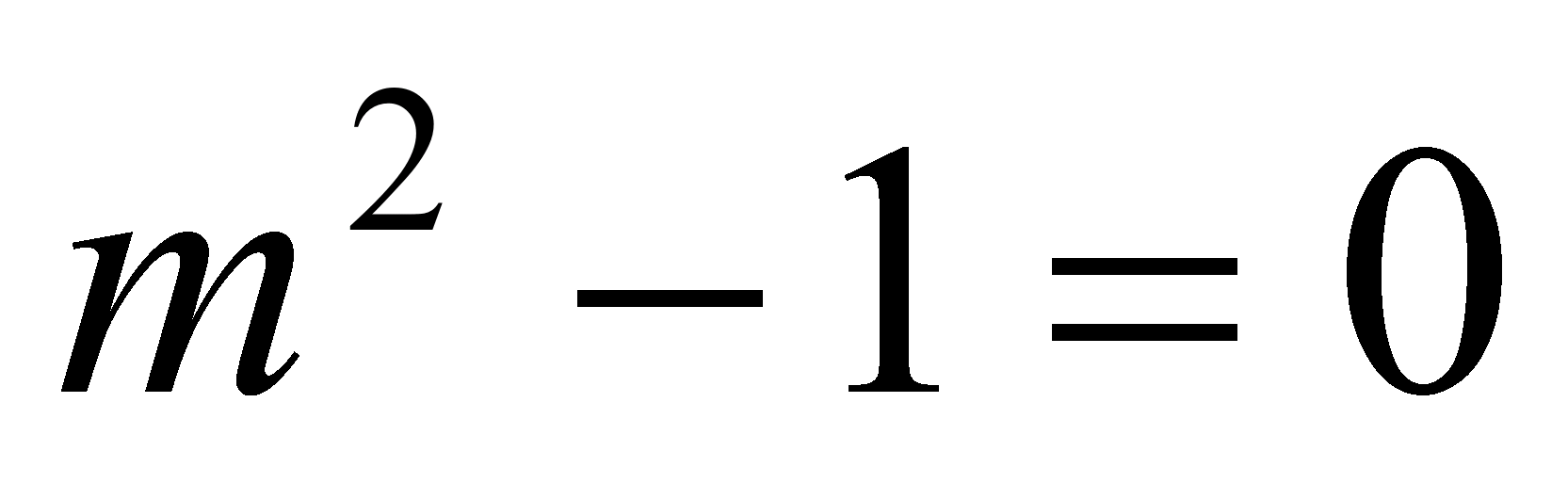 , т.е
, т.е  или
или 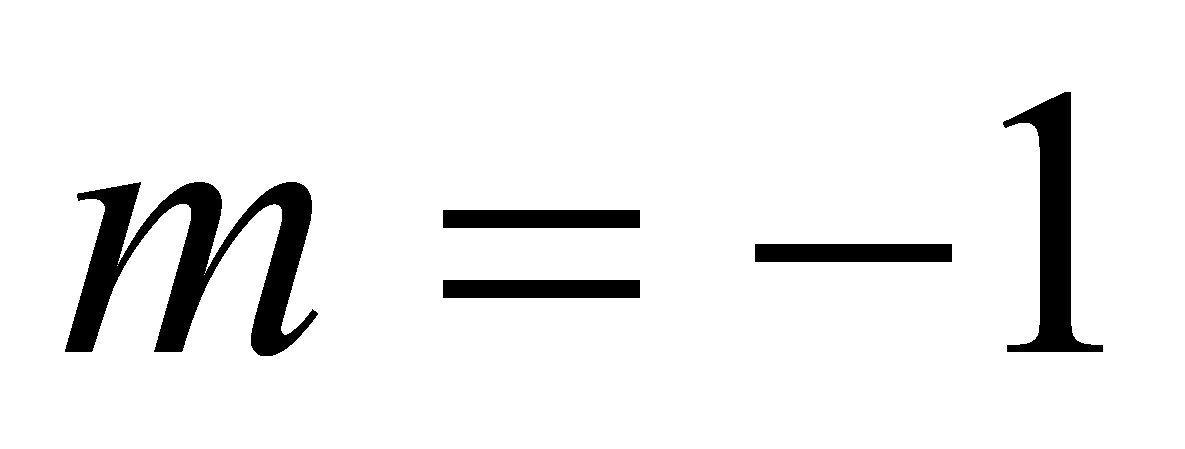 , то: 1) при
, то: 1) при  , получается уравнение
, получается уравнение 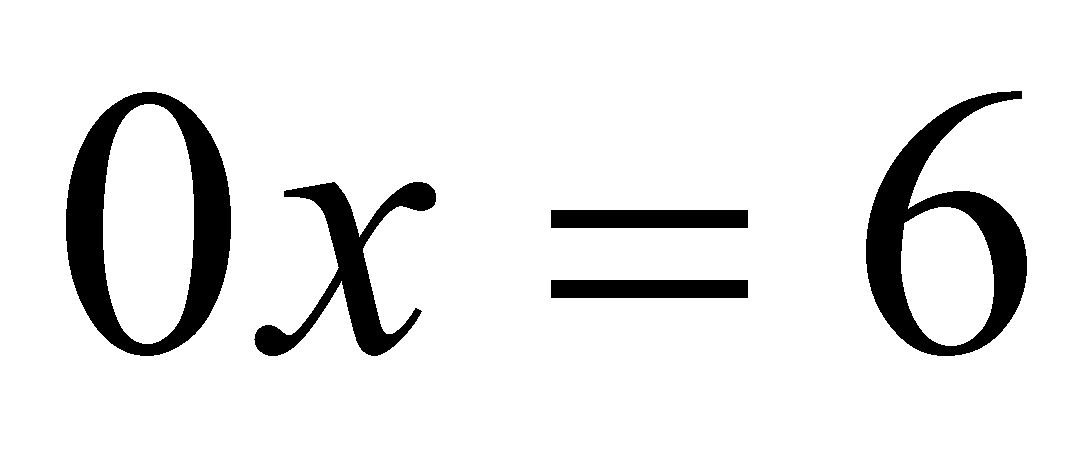 , которое корней не имеет; 2) при
, которое корней не имеет; 2) при 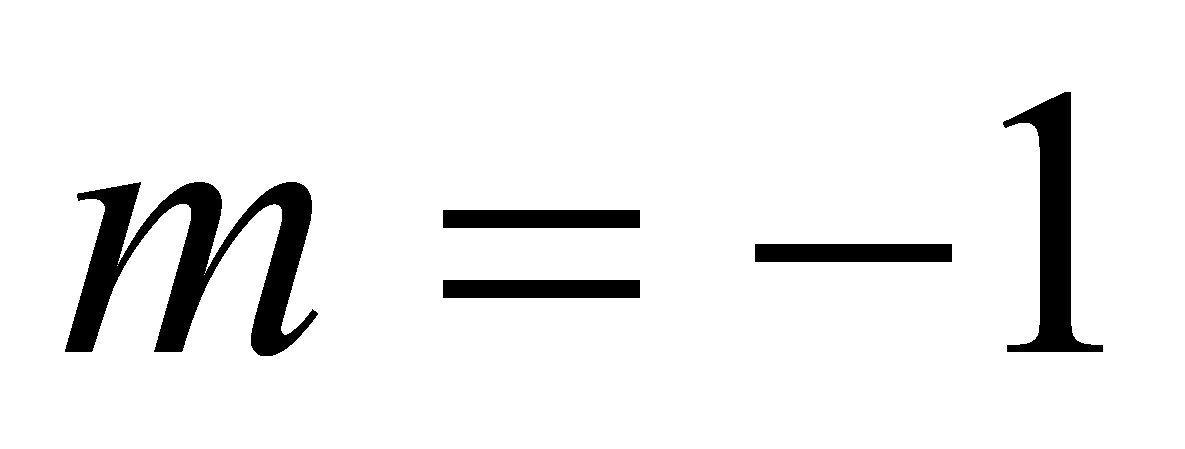 , получается уравнение
, получается уравнение 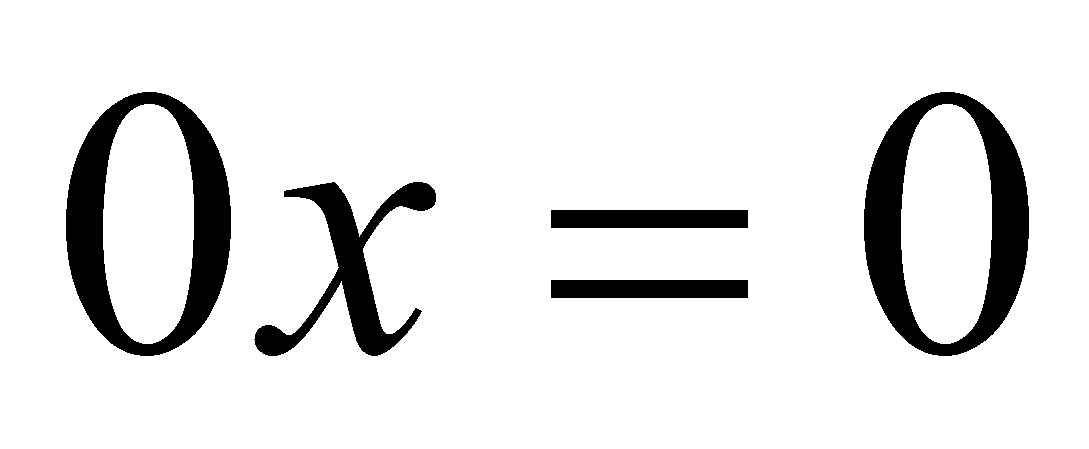 , корнем которого является любое число.
, корнем которого является любое число.
Ответ: 1) ![]() и
и ![]() ,
, ![]() ;
;
2) ![]() , нет корней;
, нет корней;
3) ![]() ,
, ![]() - любое число.
- любое число.
Пример 4: ![]()
После преобразования получаем равносильное данному уравнение:
![]() .
.
-
Если
 , то
, то 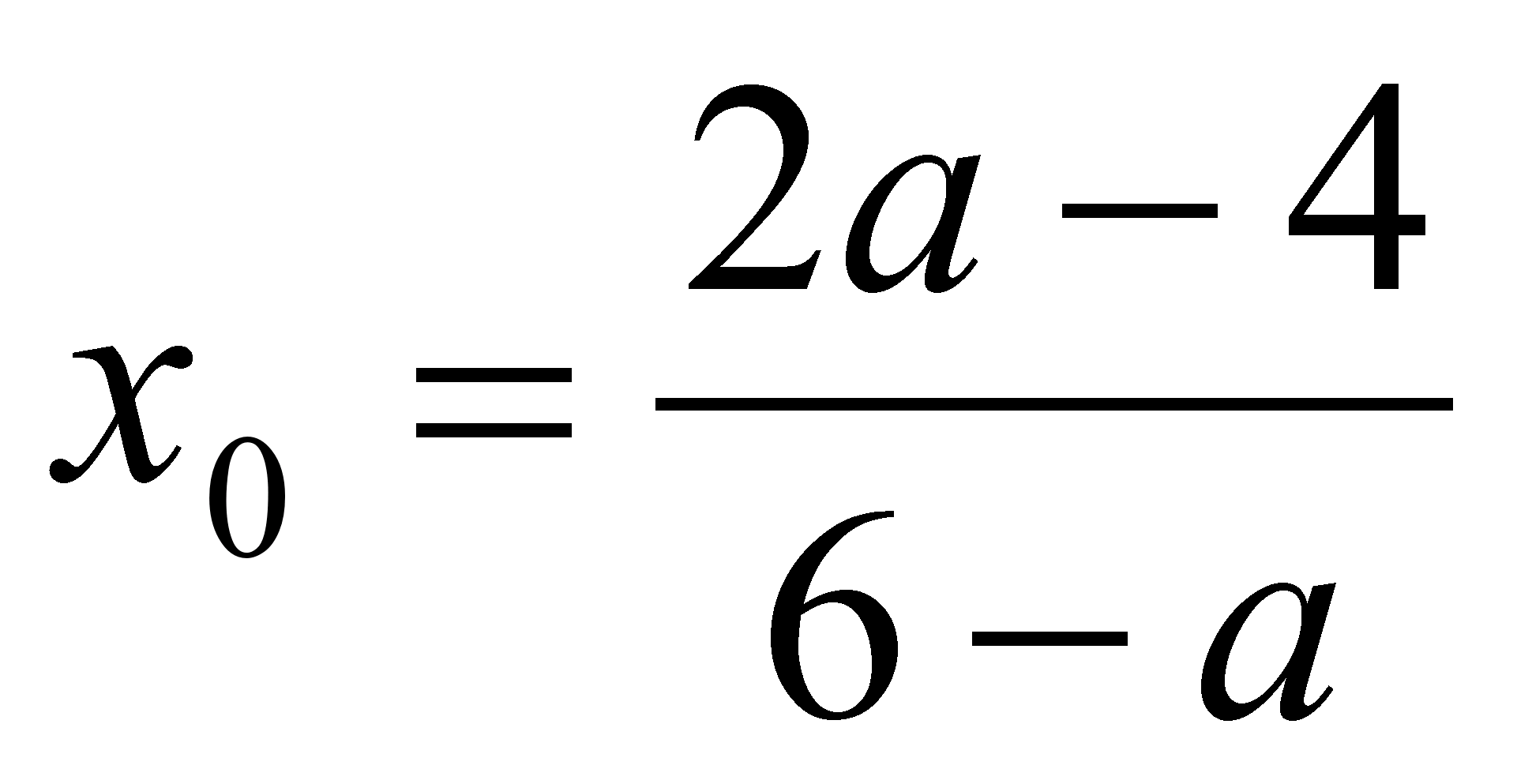
-
Если
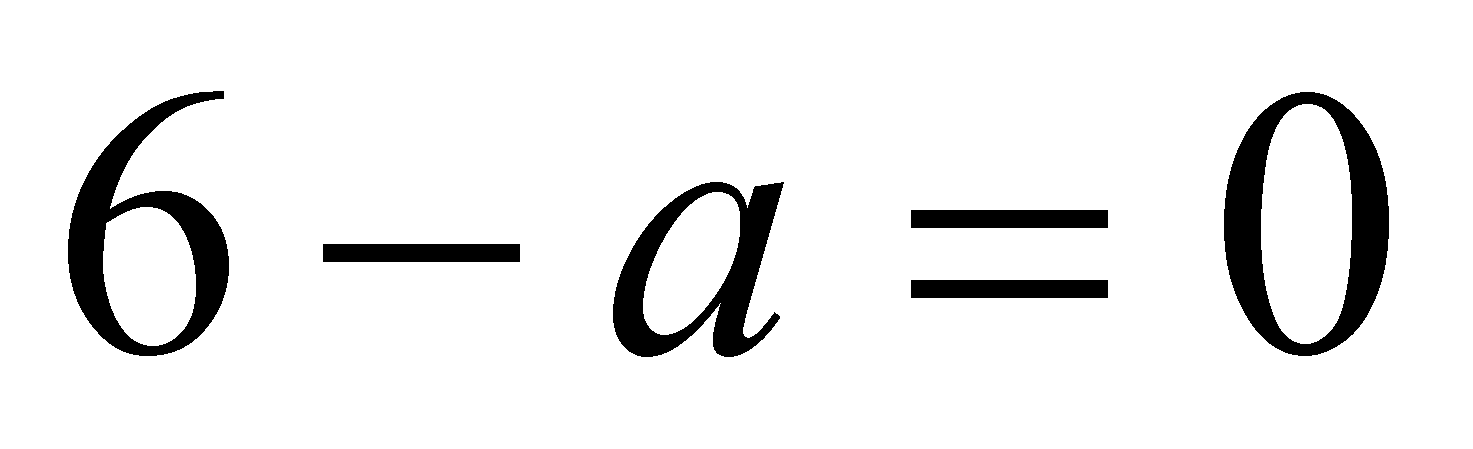 , т.е .
, т.е . 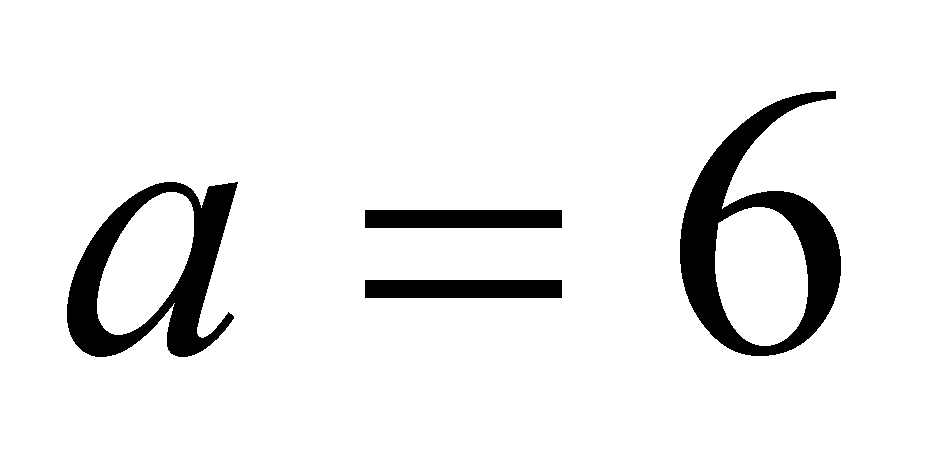 , то нет корней
, то нет корней
Ответ: Если ![]() , то
, то ![]() ;
;
Если ![]() , т.е
, т.е ![]() , то нет корней
, то нет корней
Пример 5: ![]() (1)
(1)
После преобразования получаем равносильное данному уравнение:
![]() ,
, ![]() ,
,
-
Если
 и
и  , то получаем
, то получаем  ;
; -
Если
 , то
, то 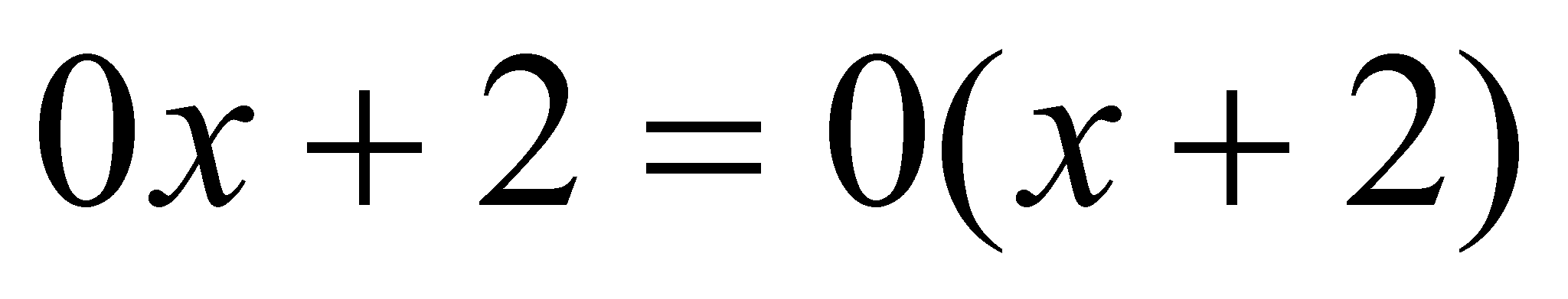 , следовательно уравнение (1) не имеет решения;
, следовательно уравнение (1) не имеет решения; -
Если
 , то получаем
, то получаем  , т.е.
, т.е.  , значит
, значит  - любое;
- любое;
Ответ: 1) ![]() и
и ![]() ,
, ![]() ;
;
2) ![]() , нет корней;
, нет корней;
3) ![]() ,
, ![]() - любое.
- любое.
Пример 6. Решить уравнение
2а•(а-2)•х = а-2. (2)
Решение.
Рассмотрим случаи:
1) При а=0 уравнение (2) принимает вид 0•х=2. Это уравнение не имеет корней.
2) При а=2 уравнение (2) принимает вид 0•х=0. Корнем этого уравнения является любое действительное число.
3) При а≠0, а≠2 уравнение соответствует третьему типу откуда х =![]() =
=![]() .
.
0твет: 1) если а=0, то корней нет;
2) если а=2, то х — любое действительное число;
3) если а≠0, а≠2 , то х = ![]() .
.
Пример 7: ![]()
Преобразуем данное уравнение: ![]() ;
;
![]() ;
;
![]() ;
;
-
Если
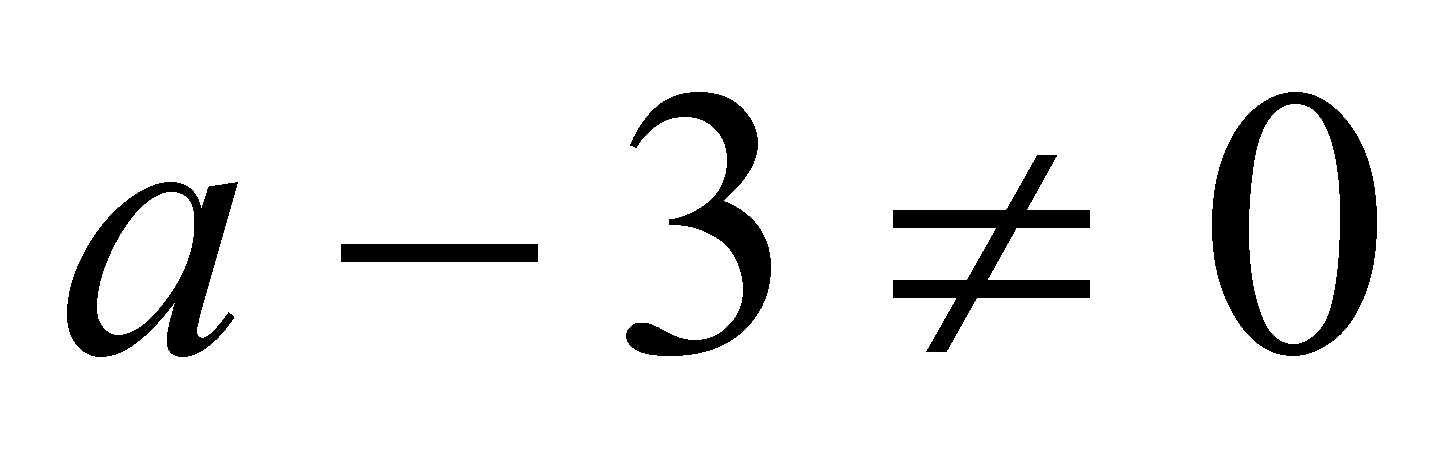 , т.е.
, т.е.  , то
, то 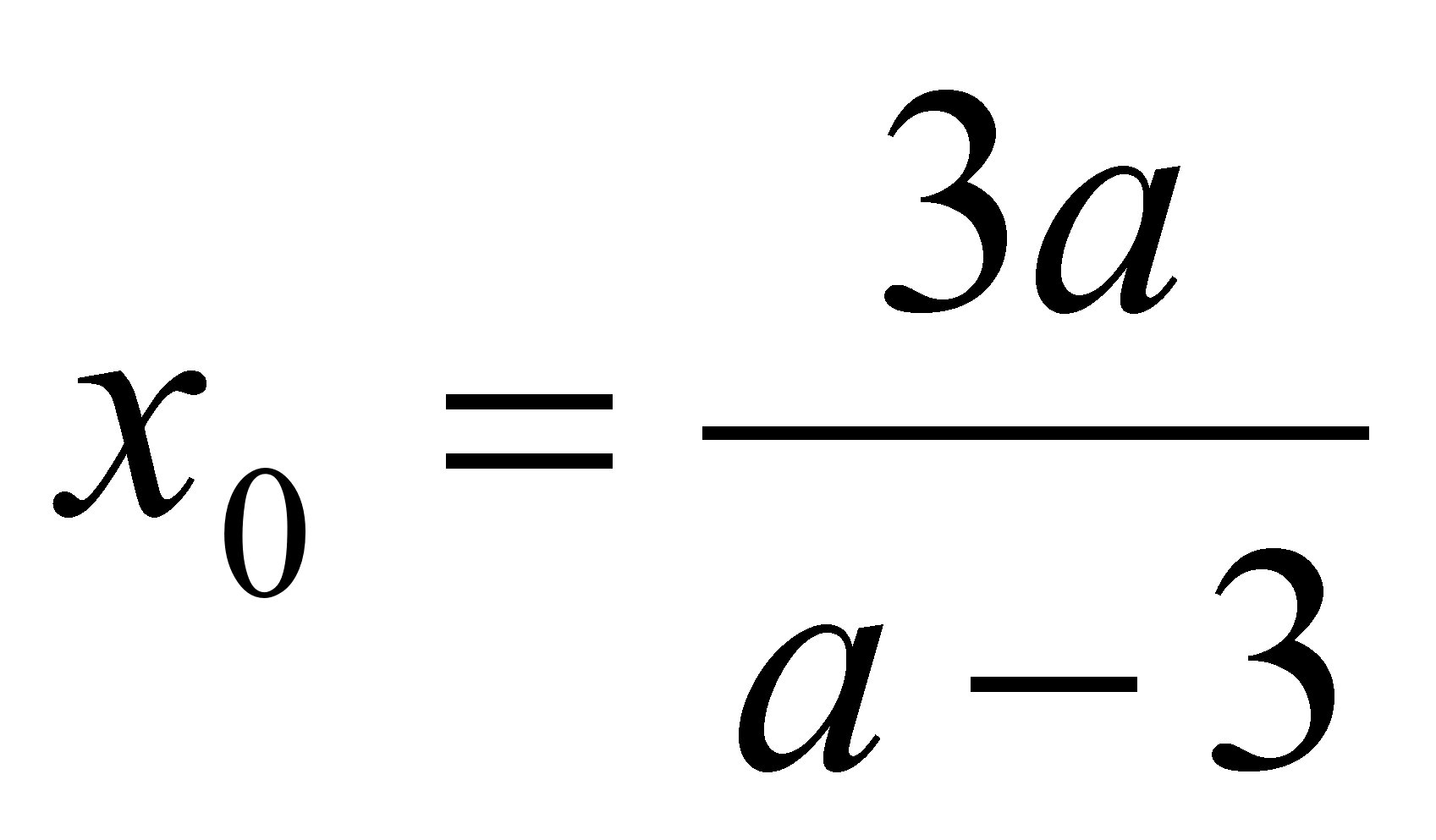 ;
; -
Если
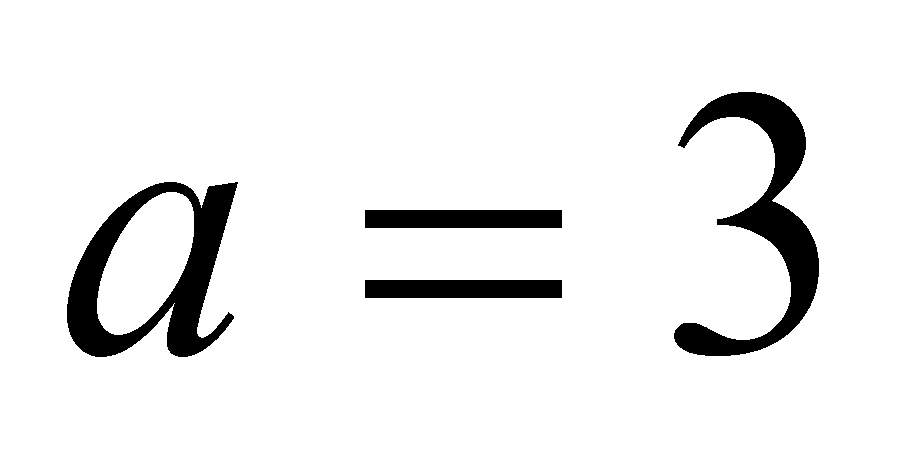 , то
, то 
 ;
;
![]() ;
;
![]() , нет корней.
, нет корней.
Ответ: 1) ![]() ,
, ![]() ;
;
2) ![]() , нет корней.
, нет корней.