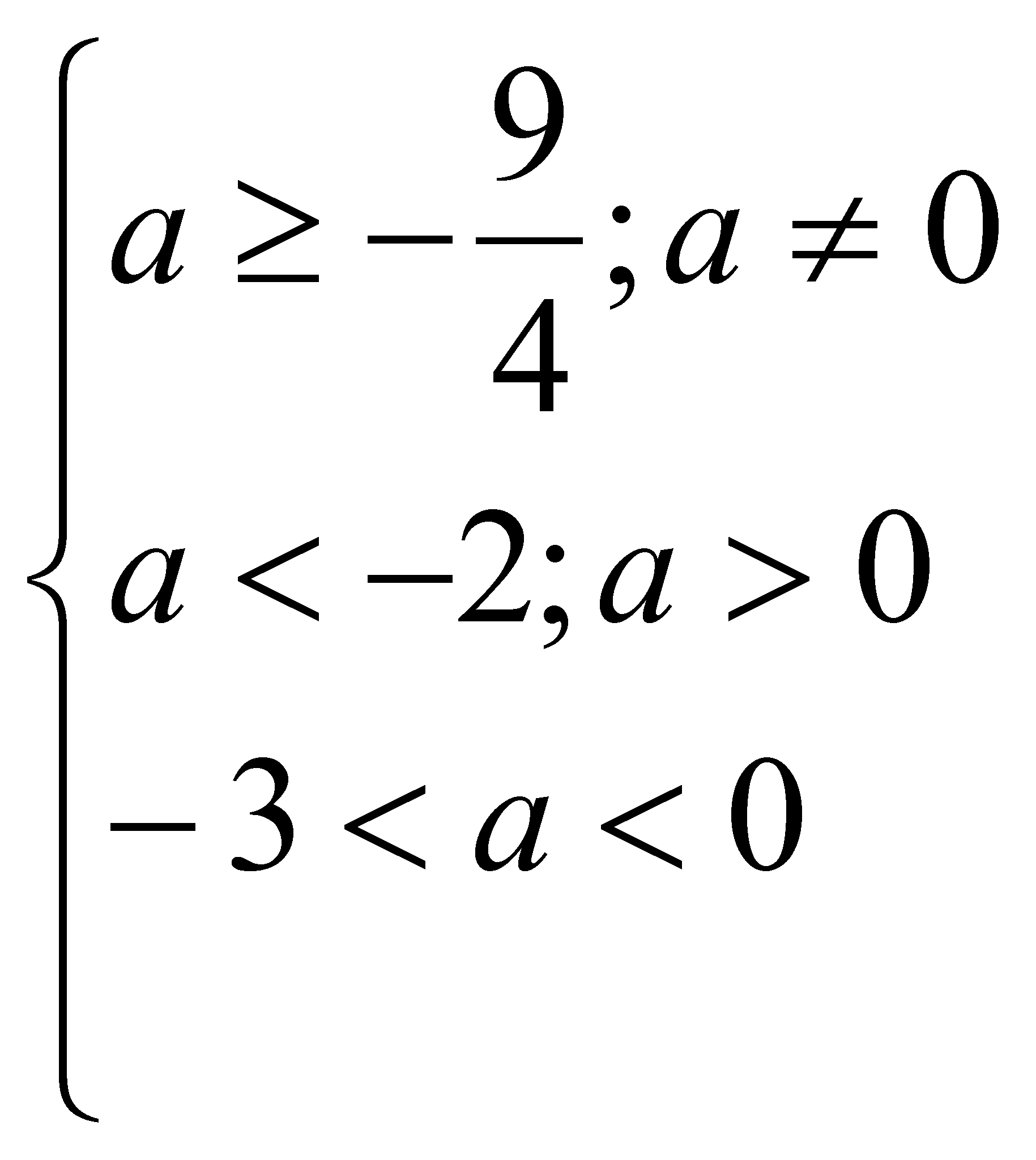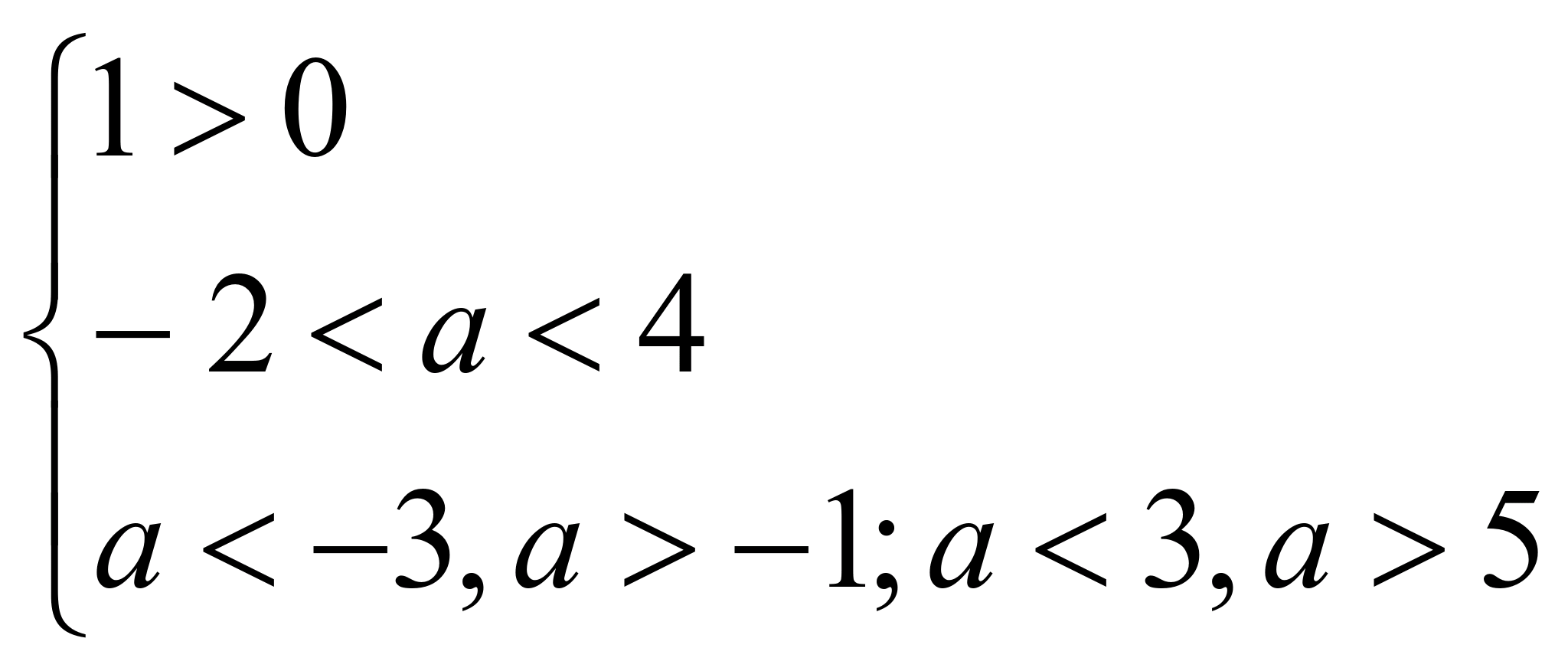Квадратные уравнения
![]() - общий вид. Его решение в действительных числах состоит из следующих частей:
- общий вид. Его решение в действительных числах состоит из следующих частей:
-
Если
 , то могут быть случаи:
, то могут быть случаи:-
Дискриминант
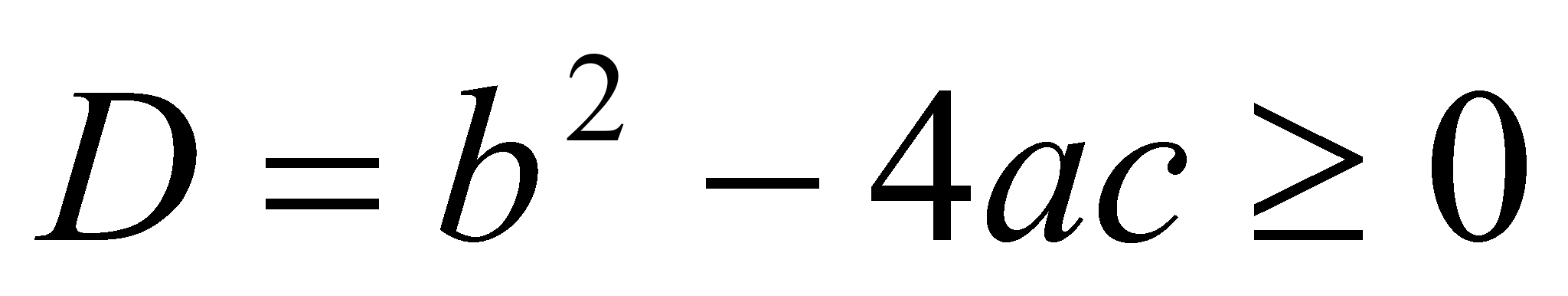 , уравнение имеет два корня (отдельно не выделяем здесь случай равенства корней при
, уравнение имеет два корня (отдельно не выделяем здесь случай равенства корней при 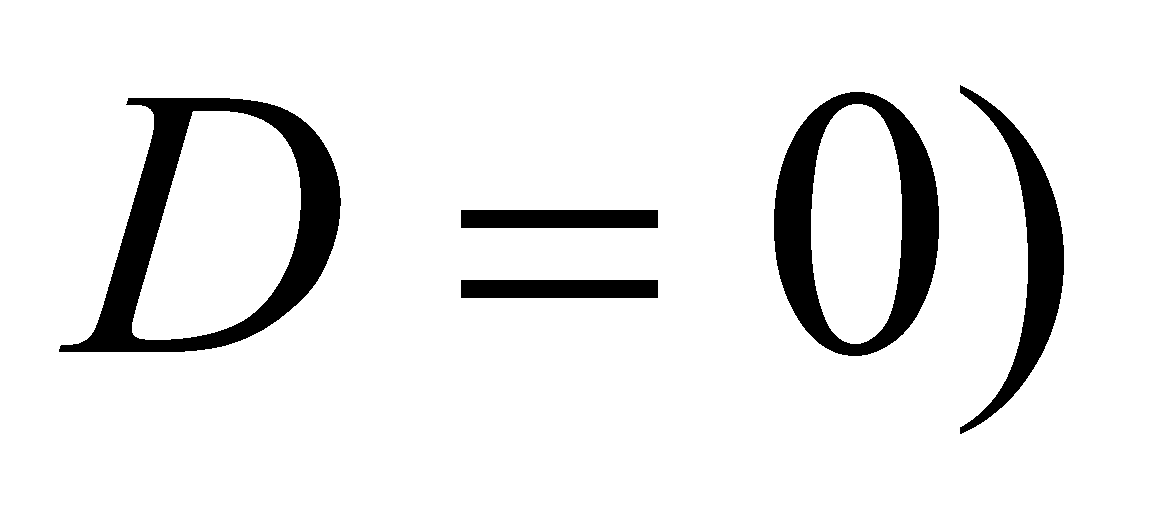
-
![]() и
и ![]() ;
;
2) ![]() , уравнение корней не имеет.
, уравнение корней не имеет.
2. Если ![]() , то уравнение превращается в линейное уравнение
, то уравнение превращается в линейное уравнение
![]() , решение которого показано выше.
, решение которого показано выше.
Результатом решения квадратного уравнения служит Ответ:
1) ![]() ,
, ![]() ,
, ![]() ;
;
2) ![]() и
и![]() ; или
; или ![]()
![]()
![]() , уравнение корней не имеет;
, уравнение корней не имеет;
3) ![]() ,
, ![]() и с – любое,
и с – любое, ![]() ;
;
4) ![]() ,
, ![]() ,
, ![]() ,
, ![]() - любое число.
- любое число.
Пример 1. Решить относительно х:
| |
(1) |
Решение: 1. Если а = 0, то –2х+4 = 0 х = 2;
2. Если а = 0, то D = 1– 4а; при 1– 4а < 0 ; а > ![]() х ? ?;
х ? ?;
при 1– 4а ? 0 ? а ? ![]()
![]() .
.
Ответ:1) а = 0, х = 2;
2) а > 0 и а ≠ ![]() уравнение (1) имеет два решения
уравнение (1) имеет два решения ![]() ;
;
3) при а ? 0 и а ? ![]() уравнение (1) не имеет решений.
уравнение (1) не имеет решений.
Пример 2. ![]() .
.
1. ![]() , т.е.
, т.е. ![]() и
и ![]() ;
; ![]() при любом значении а, значит уравнение имеет два действительных корня :
при любом значении а, значит уравнение имеет два действительных корня :
![]() ,
, ![]() ,
, ![]() .
.
2. ![]() т.е.
т.е. ![]() или
или ![]() :
:
1) ![]() ,
,![]() , корень
, корень ![]() ;
;
2) ![]() ,
, ![]() , корень
, корень ![]() .
.
Ответ: 1) ![]() и
и ![]() ,
, ![]() ,
, ![]() ;
;
2) ![]() ,
, ![]() ;
;
3) ![]() ,
, ![]() .
.
Пример 3: ![]() .
.
1. ![]() , т.е.
, т.е. ![]() ;
; ![]() .
.
1) ![]() т.е.
т.е. ![]() , уравнение имеет два действительных корня
, уравнение имеет два действительных корня ![]() ;
;
2) ![]() , т.е. при
, т.е. при ![]() и
и ![]() уравнение действительных корней не имеет.
уравнение действительных корней не имеет.
2. ![]() , т.е.
, т.е. ![]() получается уравнение линейное с единственным корнем
получается уравнение линейное с единственным корнем ![]() .
.
Ответ: 1) ![]() или
или ![]() ,
, ![]() ;
;
2) ![]() ,
, ![]() ;
;
3) ![]() и
и ![]() , корней нет.
, корней нет.
Пример 4. Решить уравнение
![]() =0 (2)
=0 (2)
Решение:
1) ![]() , т.е.
, т.е. ![]() , уравнение (2) примет вид
, уравнение (2) примет вид ![]() . Из этого уравнения находим х = –
. Из этого уравнения находим х = – ![]() .
.
2)![]() , т.е.
, т.е. ![]() ;
; ![]() , т. е.
, т. е. ![]() , получаем х1,2
, получаем х1,2 ![]()
3) Если ![]() , уравнение не имеет корней;
, уравнение не имеет корней;
4) Если ![]() , то
, то ![]() и тогда
и тогда ![]() .
.
Ответ: 1) если ![]() , то корней нет;
, то корней нет;
2) если а = 1, то х =![]() ;
;
3) если ![]() , то
, то ![]() ;
;
4) если 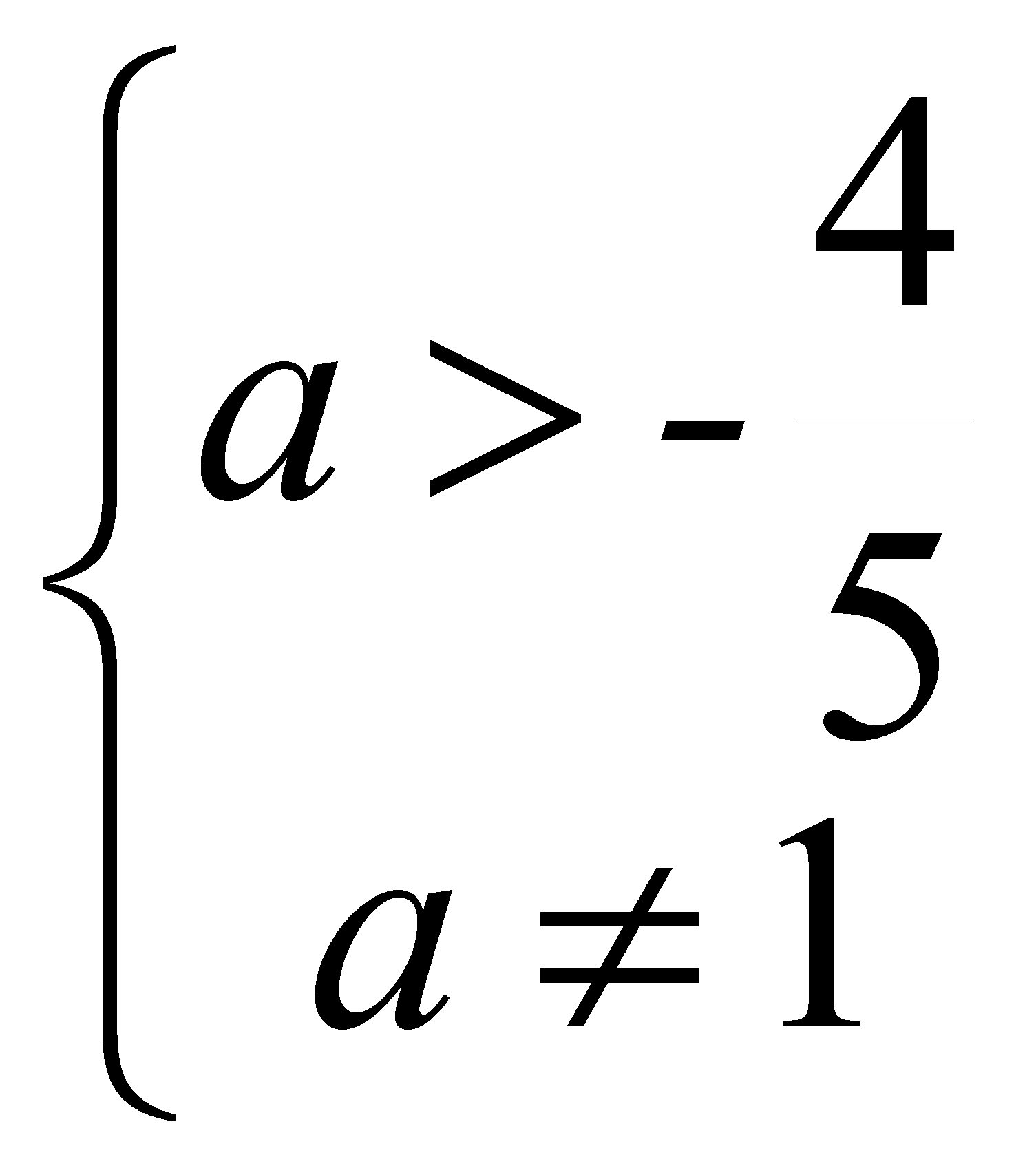 , то
, то 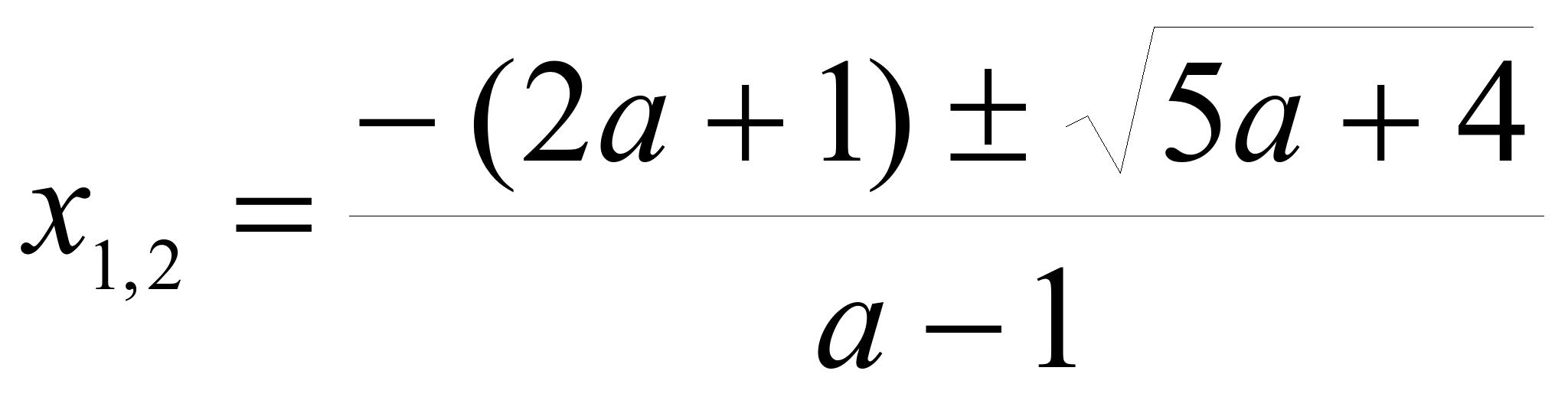 .
.
Пример 5. ![]()
Решение:
1. ![]() при любом значении а; значит уравнение имеет два действительных корня
при любом значении а; значит уравнение имеет два действительных корня
![]() ;
; ![]() .
.
Ответ: ![]() ,
, ![]() при любом а.
при любом а.
Пример 6. ![]()
Решение: 1. ![]() , т.е.
, т.е. ![]() и
и ![]() ;
;
![]() при любом значении а; значит уравнение имеет два действительных корня
при любом значении а; значит уравнение имеет два действительных корня
![]() ;
; ![]() .
.
2. ![]() , т. е.
, т. е. ![]() или
или ![]()
1) ![]() ,
, ![]() - корень;
- корень;
2) ![]() ,
, ![]() - корень.
- корень.
Ответ: 1) ![]() и
и ![]() ,
, ![]() ,
, ![]() ;
;
2) ![]() ,
, ![]() ;
;
3) ![]() ,
, ![]() .
.
При исследовании квадратичной функции мы используем теоремы, которые также помогают при решении задач с параметрами.
Т1. Если приведённое квадратное уравнение имеет два корня и b ? 0,
c ? 0, то оба корня этого уравнения отрицательные; b ? 0, c ? 0, то оба корня этого уравнения неотрицательны.
Т2. Необходимые и достаточные условия, чтобы корни квадратного уравнения были больше заданного числа d:
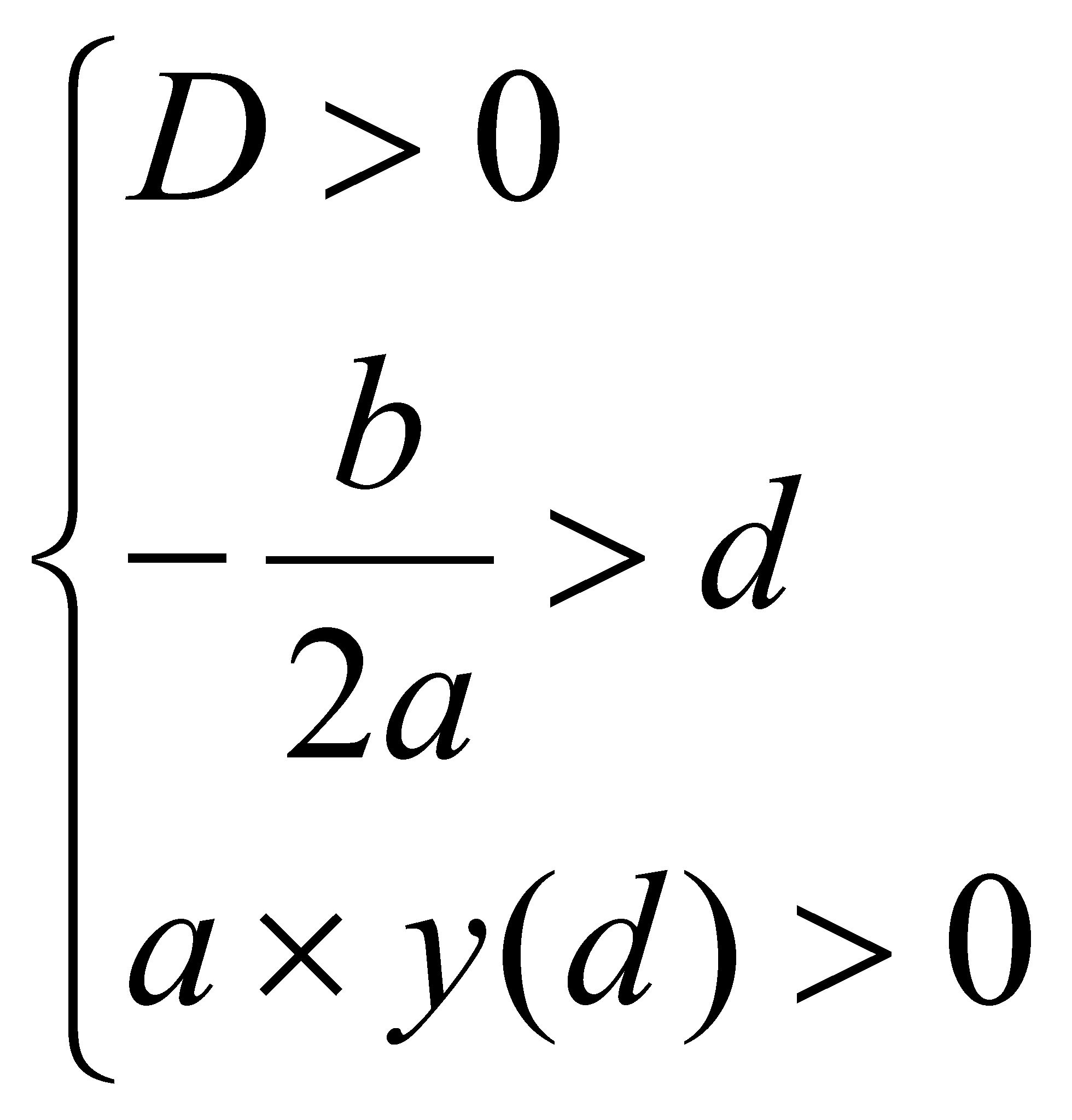
Пример 7. При каких значениях параметра а, корни уравнения неотрицательны:
| |
(1) |
Разделим уравнение (1) на а, но поставим условие а ? 0, тогда получим
| |
(2) |
По Т1: 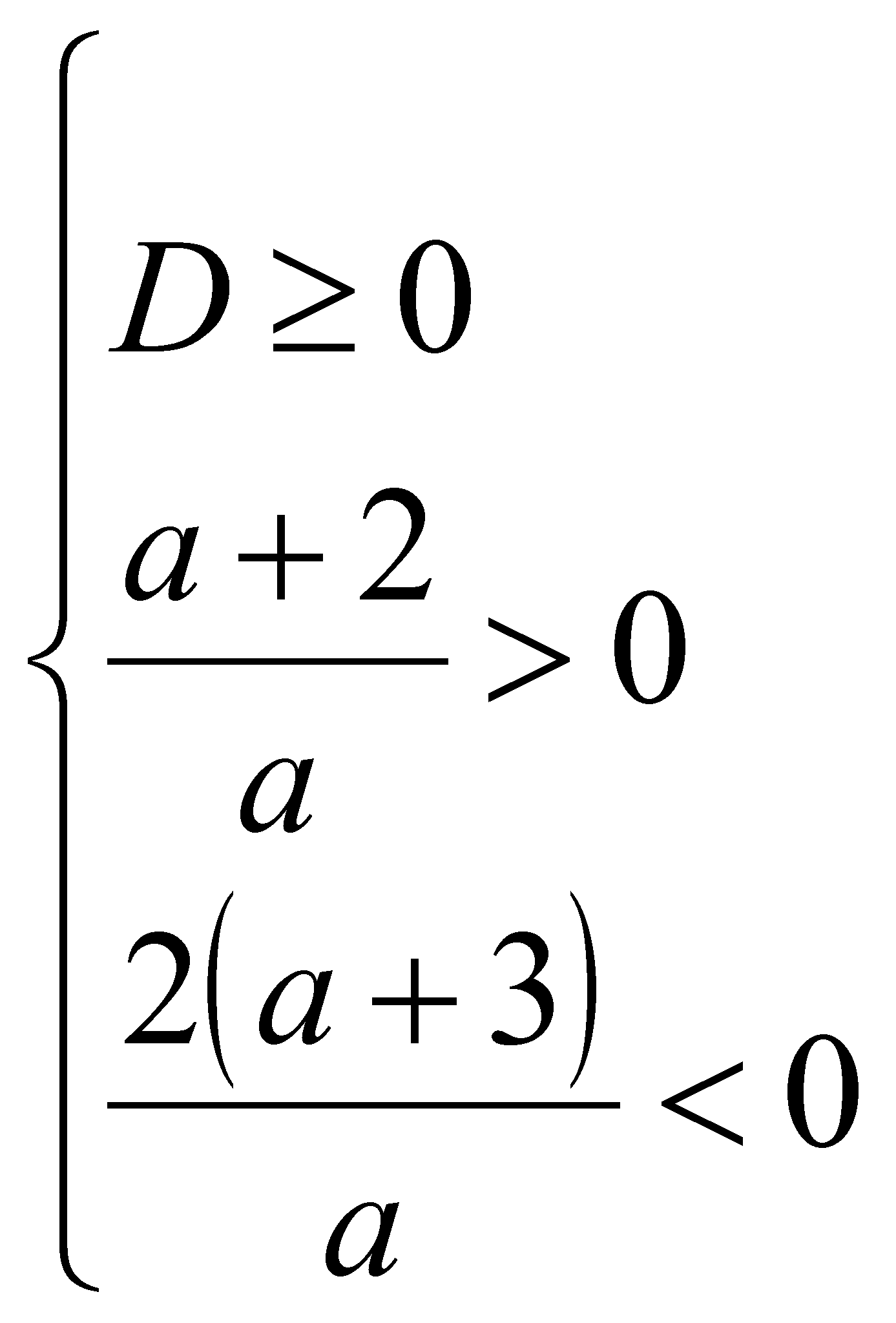 ;
;
1). D = ![]() ; приводим к общему знаменателю а2, получаем
; приводим к общему знаменателю а2, получаем
![]() ;
; ![]() .
.
2
![]() ? 0; корень уравнения
? 0; корень уравнения ![]() : а = –2 и а ? 0. Получаем а ? –2, а ? 0
: а = –2 и а ? 0. Получаем а ? –2, а ? 0
3
). ![]() ; корень уравнения
; корень уравнения ![]() : а = –3
: а = –3
и
4
| |
|
Получаем ![]()
Ответ: при ![]() уравнение (1) имеет неотрицательные корни.
уравнение (1) имеет неотрицательные корни.
Пример 8. При каких значениях параметра а, корни уравнения больше 1:
| |
|
По Т2: 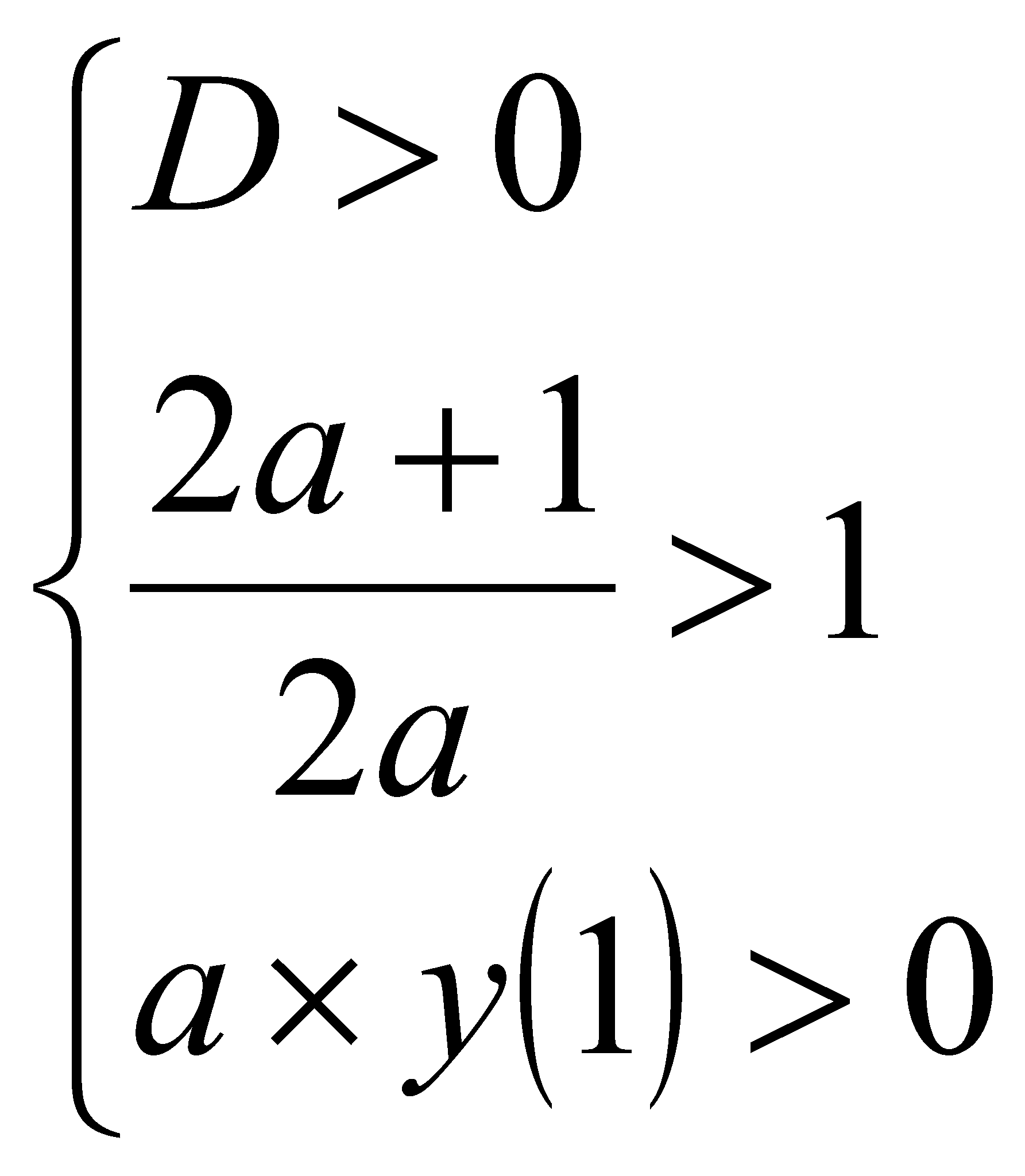 .
.
1) ![]()
![]() ? 0, разделим получившееся неравенство на –8, получаем
? 0, разделим получившееся неравенство на –8, получаем
![]()
![]() .
.
П
олучаем  ? а ?
? а ? 
2) ![]() , помножим обе части данного неравенства на 2а, при этом а ? 0;
, помножим обе части данного неравенства на 2а, при этом а ? 0;
2а + 1 ? 2а ? 2а – 2а ? –1 ? 0 ? –1 ? а ? R.
3) y(1) = 2а –2;
![]() корни уравнения 2а(а-1) ? 0: а1 = 0; а2 = 1. П
корни уравнения 2а(а-1) ? 0: а1 = 0; а2 = 1. П
4). Объединим полученные результаты:
| |
|
П
![]()
Ответ: при 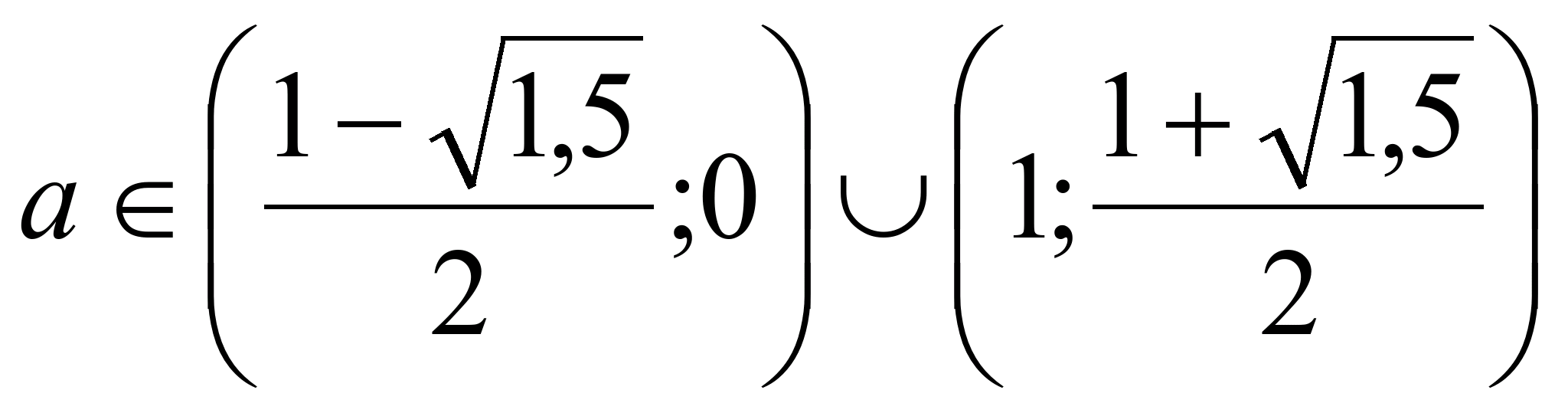 корни уравнения (1) больше 1.
корни уравнения (1) больше 1.
Пример 9: При каком наибольшем целом а оба корня уравнения заключены строго между –2 и 4:
| Способ 1: |
(1) |
![]() ; тогда корни уравнения (1):
; тогда корни уравнения (1): ![]() . Они должны быть заключены строго между –2 и 4:
. Они должны быть заключены строго между –2 и 4:
![]()
![]()
П
![]()
Способ 2:
По Т2:
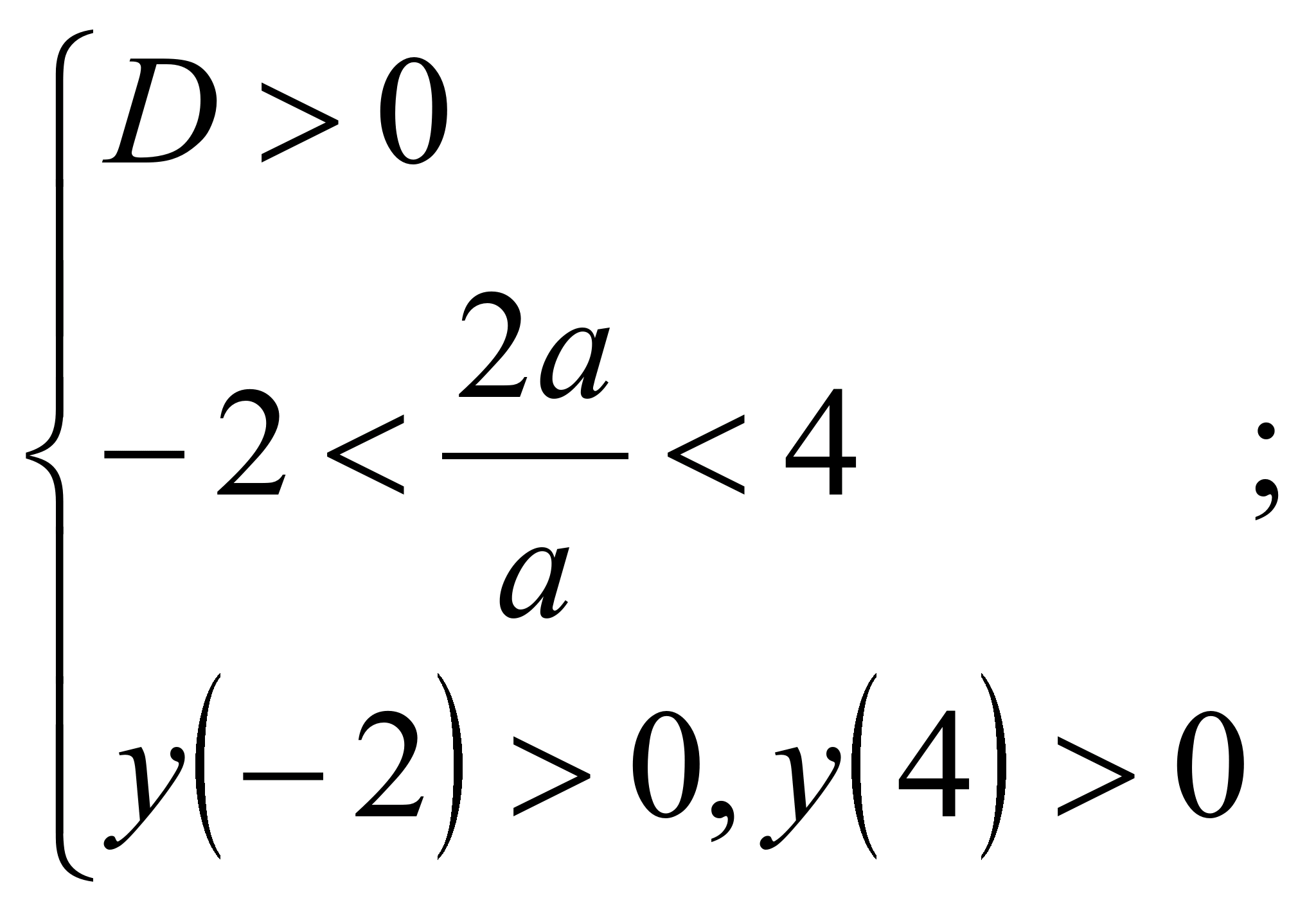
1). D = 1? 0;
2). 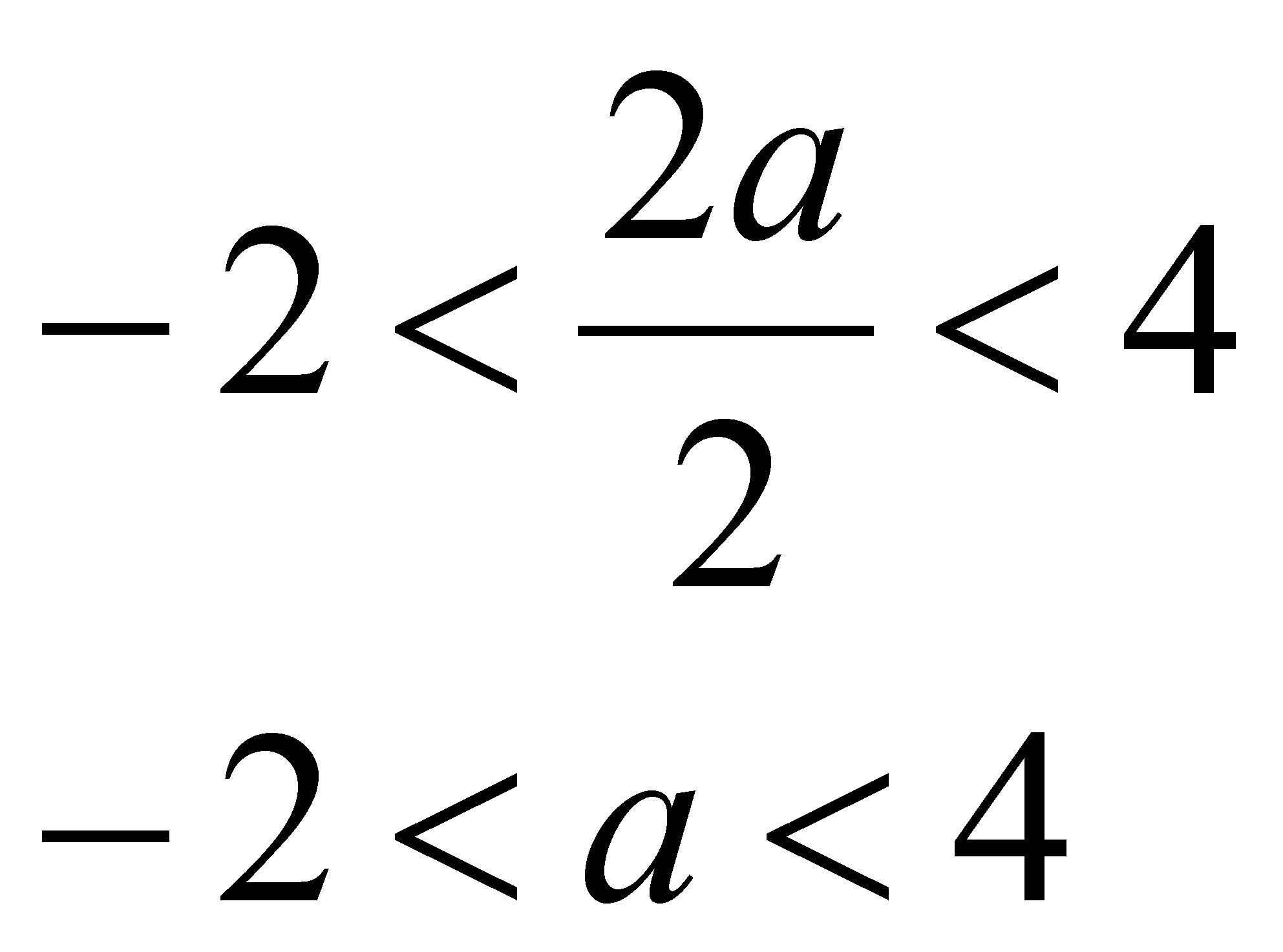 ;
;
3) y(–2) = а2+4а+3
y(4) = а2–8а+15
а
П
Рис. 9
олучаем а ? 3, а ? 5.
4). Объединим полученные результаты:
| |
|
П
Рис. 10
олучаем –1 ? а ? 3.
Ответ: при а =2 оба корня уравнения (1) заключены строго между –2 и 4.
Рассмотрим несколько задач с параметрами, используя теорему Виета:
Пусть дано уравнение ![]() и
и ![]() . Если
. Если ![]() и
и ![]() - различные корни этого уравнения, то
- различные корни этого уравнения, то ![]()
![]()
![]()
![]()
![]() ;
;
Если уравнение имеет единственный корень ![]() , то теорема Виета остается верной, если положить
, то теорема Виета остается верной, если положить ![]() .
.
Корни приведенного квадратного уравнения x2 + px + q = 0 связаны с его коэффициентами формулами Виета
х1 + х2 = - p,
х1х2 = q.
В случае, если приведенное квадратное уравнение имеет действительные корни, формулы Виета позволяют судить как о знаках, так и об относительной величине корней квадратного уравнения, а именно:
Если q > 0, p > 0, то оба корня отрицательны;
Если q > 0, p < 0, то оба корня положительны;
Если q < 0, p > 0, то уравнение имеет корни разных знаков, причем отрицательный корень по абсолютной величине больше положительного корня;
Если q < 0, p < 0, то уравнение имеет корни разных знаков, причем отрицательный корень по абсолютной величине меньше положительного корня.
Пример 10. При каких значениях параметра а уравнение
х2 + 2(а + 1) х +9а – 5 = 0 имеет два различных отрицательных корня?
Решение: Так как уравнение должно иметь два различных корня х1 и х2, его дискриминант должен быть положительным. Имеем D = 4(a + 1)2 – 4(9a – 5) = 4a2 – 28a + 24 = 4(a – 1)(a – 6). Значит должно выполняться неравенство ![]()
По теореме Виета:
х1 + х2 = - 2(а + 1),
х1х2 = 9а – 5.
Поскольку по условию х1 < 0 и х2 < 0, то – 2(а + 1) < 0 и 9а – 5 < 0.
Приходим к неравенствам: 1) 4(а – 1)(а – 6) > 0, т. е. а < 1; a > 6;
-
- 2(a + 1) < 0, т. е. а > - 1;
-
9a – 5 > 0, т. е. а >
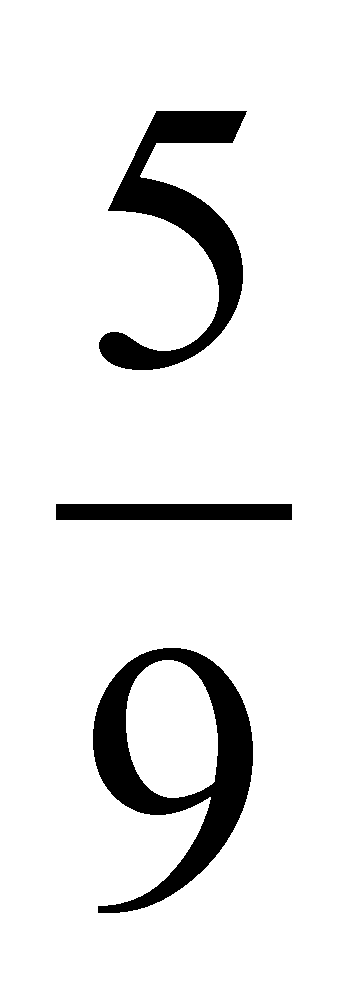
Ответ: ![]() < a < 1, либо а > 6.
< a < 1, либо а > 6.
Пример 11. Найти коэффициент а, если корни уравнения связаны соотношением 2х1+х2 = 3:
![]()
по теореме Виета:  ; составим и решим систему:
; составим и решим систему:  получаем х1 = 1, х2 = 1, тогда а = 1.
получаем х1 = 1, х2 = 1, тогда а = 1.
Ответ: а = 1.